1. Il Museo e la Biblioteca

[pag.354]

◗ Alessandria capitale culturale del mondo ellenistico

In un precedente capitolo abbiamo già menzionato il sorgere di nuovi centri culturali a Pergamo, Rodi, e, soprattutto, ad Alessandria. Atene riuscì a mantenere ancora il suo primato nel campo della filosofia, ma Alessandria divenne il grande centro della cultura scientifica, che proprio qui raggiunse le più alte vette toccate nel mondo antico.
I lavori di costruzione della città, voluta da Alessandro a memoria del proprio nome, iniziarono nel 332 a.C. e durarono a lungo. La posizione era stata scelta con un intuito infallibile: infatti, trovandosi presso le foci del Nilo, essa assommava, a un tempo, i benefici provenienti dalla coltivazione del fertile retroterra e dal commercio. La popolazione crebbe rapidamente e agli elementi locali si aggiunsero quelli provenienti da ogni parte, fra i quali sono da segnalare soprattutto gli Ebrei. L’elemento greco, naturalmente, fu quello prevalente: ma è proprio in questo contesto cosmopolitico che la dimensione culturale propriamente ellenica si dilatò nel senso ellenistico che è già stato spiegato. Tolomeo, figlio di Lago, dopo la morte di Alessandro, ottenne il governo dell’Egitto e i suoi successori lo mantennero a lungo, conservando quelle tradizionali strutture socio-politiche che avevano assicurato vita millenaria al paese. Essi impedirono quindi l’ellenizzazione dell’Egitto, con la sola eccezione di Alessandria, in cui, al contrario, cercarono di attrarre gli intellettuali greci, nel tentativo di trasformarla con ogni mezzo in capitale culturale del mondo ellenistico. Nacque, così, una città modernissima in uno Stato dalla struttura orientale, la quale ebbe un destino, si può dire, unico o, per lo meno, del tutto eccezionale.
Già a partire all’incirca dal 297 a.C., Demetrio Falereo, che proveniva dalle file dei peripatetici, e che per ragioni politiche aveva dovuto rifugiarsi ad Alessandria, ebbe con Tolomeo_I_Soter intensi contatti, che divennero via via più stretti. Demetrio pensò di fondare in Alessandria qualcosa che fosse come un Peripato di proporzioni moltiplicate, costruito e adattato in base alle nuove esigenze. Chiamò ad Alessandria lo stesso Stratone di Lampsaco, scolarca del Peripato, che divenne addirittura precettore del figlio del re. Il disegno di Demetrio e di Tolomeo era quello di raccogliere in una grande istituzione tutti i libri e tutti gli strumenti scientifici necessari alle ricerche, in modo da fornire agli studiosi un materiale che non avrebbero potuto trovare da nessun’altra parte e indurli così a venire ad Alessandria.
Nacquero, in tal modo, il Museo (che significa “Istituzione sacra alle Muse”, protettrici delle attività intellettuali) e l’annessa Biblioteca. Il primo offriva tutte le attrezzature per le indagini mediche, biologiche, astronomiche; la seconda offriva l’intera produzione letteraria del mondo greco. Con Tolomeo II la Biblioteca si avviò all’imponente cifra di 500.000 libri, che via via si accrebbe fino a 700.000, costituendo la più grandiosa raccolta di libri del mondo antico. [pag.355]
La Biblioteca ebbe famosi direttori. Ci sono pervenuti tutti i nomi del periodo aureo: Zenodoto, Apollonio Rodio, Eratostene, Aristofane di Bisanzio, Apollonio_Eidografo, Aristarco di Samotracia. Questi uomini, come vedremo, gettarono le basi della scienza filologica per i secoli a venire. Il Museo attrasse, invece, matematici, astronomi, medici, geografi, i quali espressero, nell’ambito di questa istituzione, il meglio di quanto l’antichità abbia prodotto, come vedremo più avanti.

◗ La nascita della filologia

Zenodoto, che fu il primo bibliotecario, iniziò la sistemazione dei volumi, ma fu Callimaco che, sotto il regno di Tolomeo II (283-247), compilò i Pinakes ossia i Cataloghi (in 120 libri), in cui ordinò i volumi per settori e generi letterari, con ordinamento alfabetico degli autori, breve biografia dei medesimi, sistemazione della produzione dei singoli autori, soluzione dei problemi delle attribuzioni dubbie. I Cataloghi di Callimaco furono la base di tutto il lavoro successivo.
Zenodoto approntò, invece, la prima edizione di Omero e fu, forse, proprio lui a dividere in 24 libri sia l’Iliade, sia l’Odissea. Anche Aristofane di Bisanzio (257-180 a.C.) e Aristarco di Samotracia (217-145 a.C.) approntarono delle edizioni di Omero . Ma è importante soprattutto Aristarco, che costituisce la principale fonte della nostra tradizione. I controlli dei numerosi esemplari posseduti dalla Biblioteca lo portarono a individuare e a espungere versi interpolati e a segnalare quelli sospetti. Ai suoi commenti attinsero gli scoliasti posteriori.
Dionigi di Tracia , discepolo di Aristarco, compose la prima Grammatica greca a noi nota, beneficiando dell’apporto che, in questo campo, avevano dato peripatetici e stoici (nel 145 riparò a Rodi, cacciato da Tolomeo Fiscone ). L’interpretazione allegorica di Omero e di altri poeti fu, invece, codificata da Cratete_di_Mallo a Pergamo, e da allora a poco a poco si diffuse e si rafforzò (fu adottata, tra l’altro, dagli stoici), fino a diventare predominante in età imperiale. In questo periodo si diffonde anche il genere letterario della biografia, di cui poco è rimasto, ma che, per quanto concerne i filosofi, conosciamo almeno nella tarda esemplificazione riassuntiva di Diogene_Laerzio , che ha ampiamente utilizzato molto del materiale raccolto in questo periodo.
Ricordiamo, infine, che da questo movimento filologico e dalle sue acquisizioni è stata resa possibile l’edizione delle opere esoteriche di Aristotele, di cui abbiamo detto sopra con ampiezza. Le moderne raffinatissime tecniche delle edizioni critiche di testi antichi hanno, dunque, nell’Alessandria ellenistica le loro radici storiche.

[pag.356]

2. La fioritura delle scienze particolari

Le matematiche: Euclide e Apollonio

Data l’impostazione propria del pensiero greco, la matematica è senza dubbio la scienza che godette di maggior stima, da Pitagora a Platone . Ricordiamo che la tradizione vuole che all’ingresso dell’Accademia Platone avesse fatto incidere la scritta: «Non entri chi non conosce la geometria». E abbiamo visto quale ruolo e quale peso abbia giocato la matematica sia fra i pitagorici sia nel Platonismo.
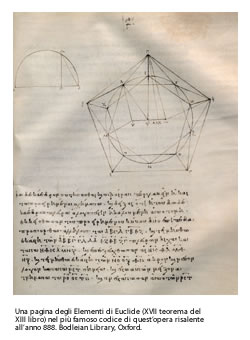
Toccò a Euclide , uno dei primi scienziati trasferitisi ad Alessandria, l’onore di redigere la summa del pensiero matematico greco, in quegli Elementi il cui impianto concettuale resse praticamente fino al secolo XIX. Della vita di Euclide non sappiamo quasi nulla. Tutti i dati in nostro possesso ci spingono a collocare l’apice della sua attività intorno al 300 (i termini 330-277 a.C. sono convenzionalmente assunti come probabili).
Ci sono state conservate anche altre opere euclidee (i Dati, l’Ottica, Sulle divisioni, giuntaci nella traduzione araba), ma meno significative. Se fosse vero un aneddoto riferito da Proclo, il suo carattere ne risulterebbe perfettamente illuminato: avendogli domandato il re Tolomeo se non ci fosse una via un po’ più semplice per introdursi alla matematica, Euclide rispose: «Nelle matematiche non ci sono vie regie».
Il procedimento degli Elementi è quello del discorso assiomatico, ossia quello secondo cui, poste certe cose, ne seguono di necessità altre, strutturalmente concatenate. Le strutture della deduzione proprie della logica aristotelica risultano operanti in maniera precisa, così come il generale impianto teoretico della medesima. E poiché l’impianto della logica aristotelica prevede appunto definizioni, principi o assiomi comuni e postulati specifici per ogni scienza, così gli Elementi di Euclide presentano una serie di definizioni, cinque postulati e gli assiomi comuni. Le definizioni calibrano i termini che entrano nel discorso; gli assiomi comuni sono specificazioni del principio di non contraddizione su cui, secondo Aristotele, ci si deve fondare per sviluppare qualsiasi discorso logico; i postulati sono delle assunzioni di base, di carattere fondamentalmente intuitivo (quindi immediate, ossia non dimostrabili, non mediabili) che costituiscono il sostrato stesso della trattazione. Com’è noto, il quinto postulato ha sollevato una quantità di problemi, e, nel tentativo di risolverli, nacquero le geometrie non euclidee. Ma, poiché di queste dovremo parlare a suo tempo, qui non entreremo nei dettagli delle questioni concernenti i postulati.
Rileviamo, invece, come, fra i procedimenti argomentativi, Euclide usi spesso il metodo della riduzione all’assurdo, che non è altro se non il celebre élenchos, che ha una gloriosissima storia, che inizia addirittura con la Scuola eleatica e in particolare con i celebri argomenti di Zenone, prosegue con Gorgia e con la dialettica socratica, con Platone e con Aristotele .
Accanto a questo metodo, Euclide fa uso di quello che più tardi sarà detto metodo dell’esaustione, applicato soprattutto negli ultimi libri, ma che nel decimo ha la sua prima formulazione paradigmatica: «Assumendosi come date due grandezze disuguali, se si sottrae alla maggiore una grandezza maggiore della metà, alla parte restante un’altra grandezza maggiore della metà, e così procedendo successivamente, rimarrà una grandezza che sarà minore della grandezza minore assunta». L’esempio che di solito si riporta per chiarire in modo intuitivo questa proposizione è il seguente: sia A la grandezza maggiore, ad esempio un cerchio, e B quella minore. Ora, sottraiamo al cerchio una grandezza maggiore della sua metà, ad esempio iscrivendo nel cerchio un quadrato (e sottraendo, quindi, dall’area del cerchio quella del quadrato); quindi procediamo, sottraendo alla parte restante un’altra grandezza maggiore della metà, ad esempio bisecando gli archi determinati dal lato del quadrato e quindi ottenendo un ottagono (che sottrarremo all’area del cerchio), [pag.357] e così procedendo, bisecando via via, otterremo un poligono che tende ad avvicinarsi sempre di più al cerchio, e quindi una grandezza tale che, sottratta a quella del cerchio, diverrà minore della grandezza B data, qualunque questa sia. È quindi sempre possibile trovare, per questa via, una grandezza sempre più piccola di qualunque grandezza data, per quanto piccola essa sia, perché non esiste una grandezza minima.

Attilio Frajese, storico della matematica, ha giustamente ricordato, a questo proposito, Anassagora, il quale sosteneva che c’è sempre un più piccolo del piccolo (divisibilità all’infinito delle omeomerie), così come c’è un sempre più grande rispetto a qualsiasi cosa grande. In Anassagora si trova dunque l’antecedente di questo metodo.
Si è spesso discusso sull’“originalità” del contenuto di questi Elementi. Che Euclide vi abbia convogliato tutto quanto i Greci avevano pensato in materia nei tre secoli precedenti è fuori dubbio. Ma è altrettanto fuori dubbio che la genialità sta, qui, nella sintesi; ed è soprattutto nella forma di questa sintesi che la matematica greca ha fatto storia.
Dopo Euclide, a parte Archimede, di cui diremo fra poco, il più grande matematico greco fu Apollonio di Perga , vissuto nella seconda metà del III secolo a.C. Studiò ad Alessandria, ma insegnò a Pergamo.
Di lui ci sono pervenute le Sezioni coniche. Questo argomento non era del tutto nuovo, ma Apollonio ripensò a fondo l’impostazione della materia e la espose in maniera rigorosa e sistematica, introducendo anche la terminologia tecnica per designare i tre tipi di coniche, e cioè ellisse, parabola e iperbole.
Le Sezioni coniche sono considerate dagli storici della matematica un capolavoro di prima grandezza, dato che gli stessi moderni hanno potuto aggiungere poco in materia. Se Apollonio avesse applicato le sue scoperte all’astronomia, avrebbe rivoluzionato le teorie greche delle orbite planetarie. Ma queste applicazioni, come è noto, saranno effettuate solo nell’età moderna da Keplero.

◗ La meccanica: Archimede ed Erone

Archimede e le sue opere Archimede nacque a Siracusa intorno al 287 a.C. Il padre Fidia era un astronomo. Fu ad Alessandria, ma non rimase legato all’ambiente del Museo, e visse per lo più a Siracusa, essendo unito alla casa regnante da vincoli di parentela e amicizia. Morì nel 212 a.C., trucidato durante il saccheggio della città da parte delle truppe romane comandate da Marcello . Malgrado Marcello avesse ordinato di risparmiargli la vita, in segno di onore per il grande avversario che con ingegnosissime macchine belliche aveva a lungo difeso la città, un soldato lo uccise mentre era intento nei suoi studi, come vuole la tradizione, che gli fa pronunciare, nell’estremo istante, questa frase divenuta celebre: «Noli turbare circulos meos» (“Non turbare i miei cerchi”, ma la forma originaria riferitaci da Valerio Massimo è «Noli obsecro circulum istum disturbare», “Ti prego, non disturbare questo cerchio”). Sulla sua tomba Archimede volle che, [pag.359] come simbolo, venisse incisa una sfera inscritta in un cilindro, a ricordo di alcune delle sue più significative scoperte in materia. Cicerone, allorché fu questore in Sicilia, nel 75 a.C. , ritrovò la tomba e la fece restaurare come atto di grande venerazione. Delle sue numerose opere, molte sono state conservate: Sulla sfera e sul cilindro, Sulla misura del cerchio, Sulle spirali, Sulla quadratura della parabola, Sui conoidi e sugli sferoidi, Sull’equilibrio dei piani, Sui corpi galleggianti, l’Arenario e uno scritto Sul metodo dedicato a Eratostene .
I contributi matematici, fisici e metodologici di Archimede Non sono pochi gli storici della scienza antica a ritenere Archimede il più geniale degli scienziati greci. I suoi contributi di spicco sono quelli sulla problematica della quadratura del cerchio e della rettificazione della circonferenza. Nello scritto originale Sulla misura del cerchio, di cui ci è pervenuto solo un estratto, Archimede si sarebbe spinto fino al poligono di 384 lati. Il materiale trattato nelle opere Sulla sfera e sul cilindro e Sui conoidi e sugli sferoidi, contiene importanti integrazioni degli Elementi di Euclide e costituisce tuttora un capitolo importante dei trattati di geometria. E lo stesso dicasi delle conclusioni cui è pervenuto nel suo trattato Sulle spirali.
Nei Corpi galleggianti Archimede gettò le basi dell’idrostatica. Nelle proposizioni 5 e 7 si leggono i noti principi: «Delle grandezze solide quella che è più leggera del liquido, abbandonata nel liquido, si immerge in modo che un tale volume del liquido quale è quello della parte immersa, abbia lo stesso peso della intera grandezza solida»; «Le grandezze più pesanti del liquido, abbandonate nel liquido, sono trasportate verso il basso, fino al fondo, e saranno tanto più leggere nel liquido, quanto è il peso del liquido avente tale volume quanto è il volume della grandezza solida» (è questo il noto “principio di Archimede ”).
Nell’Equilibrio dei piani gettò, invece, le basi teoriche della statica, studiando, in particolare, le leggi della leva. Immaginiamo una retta a mo’ di asta poggiante su un punto di appoggio e poniamo agli estremi due pesi uguali: a distanze uguali dal centro sono in equilibrio; a distanze ineguali, si ha un’inclinazione verso il peso che si trova a maggior distanza. Di qui Archimede giunge alla legge secondo la quale due grandezze stanno in equilibrio a distanze che siano in reciproca proporzione alle stesse grandezze. La frase con cui è passato alla storia e che si suole citare in latino: Da mihi ubi consistam et terram movebo («Dammi un punto di appoggio e ti solleverò la Terra»), definisce la grandiosità della scoperta (Archimede l’avrebbe pronunciata facendo calare in mare una gigantesca nave, con un sistema di leve. La frase è riportata da Simplicio, uno degli ultimi neoplatonici del mondo antico).
L’Arenario, invece, è importante per l’aritmetica greca. In esso Archimede escogita un sistema per esprimere numeri molto grandi, operazione che il sistema greco di indicare i numeri con le lettere dell’alfabeto aveva reso fino a quel momento impossibile. Egli calcolava, in modo volutamente provocatorio, il numero di granelli di sabbia (donde il titolo) che avrebbero potuto riempire il cosmo. Per quanto grande sia il supposto numero di granelli di sabbia (che egli peraltro calcola), si tratta pur sempre di un numero grandissimo, sì, ma determinato. Si è in passato rilevato il fatto che le dimostrazioni di Archimede siano spesso macchinose e pesanti (soprattutto quando fa uso del metodo per esaustione). Il suo scritto Sul metodo, indirizzato a Eratostene (di cui parleremo più avanti), scoperto agli inizi del XX secolo, mostra, invece, che Archimede procedeva nelle sue scoperte niente affatto con quei metodi complessi e artificiosi. Egli si affidava spesso, per giungere alle scoperte, a un metodo induttivo e intuitivo (“per via meccanica”), ossia costruendo figure, e poi passava alla riprova, dimostrando rigorosamente ciò che per quella via aveva guadagnato.
Archimede e gli studi di ingegneria Archimede fu e si ritenne un matematico, ossia uno che trattava teoreticamente i problemi e considerò di conseguenza i suoi studi di ingegneria come qualcosa di marginale. Eppure, proprio per questo, fu ai suoi tempi e dai posteri ammiratissimo, dato che le sue scoperte in questo campo colpirono la fantasia ben più delle sue difficilissime speculazioni matematiche. Le macchine balistiche escogitate per difendere Siracusa, gli apparecchi per il trasporto dei pesi, l’ideazione di una pompa per l’irrigazione basata [pag.360] sul principio della cosiddetta vite perpetua e le sue scoperte legate alla statica e all’idrostatica ne fanno il più grande ingegnere del mondo antico. La tradizione vuole che, durante l’assedio di Siracusa, abbia escogitato perfino l’uso degli specchi ustori (difficilmente si tratta di pura leggenda, dato che già Luciano di Samosata ne parla). Costruì anche un planetario, che fu poi portato a Roma e che riscosse l’ammirazione di Cicerone. La narrazione di Vitruvio sul come Archimede pervenne alla scoperta del “peso specifico” (del rapporto fra peso specifico e volume), dato quanto sappiamo circa il metodo intuitivo con cui Archimede raggiungeva le sue scoperte prima di darne ragionata prova, è quantomeno molto verosimile, anche se della sua storicità nessuno può garantire. Si racconta che Gerone, re di Siracusa, volle offrire nel tempio una corona d’oro. Ma l’orafo sottrasse una parte dell’oro sostituendolo con argento, che combinò con la restante parte d’oro nella lega. All’apparenza la corona risultò perfetta. Ma, essendo sorto il sospetto della contraffazione e non potendo Gerone dar corpo al sospetto, pregò Archimede di risolvergli il caso, riflettendovi sopra quanto occorreva. E Archimede iniziò a pensarvi intensamente, e, mentre si accingeva a fare il bagno, osservò che, entrando nella vasca (che allora era una tinozza), usciva acqua in proporzione al volume del corpo che entrava. Intuì così di colpo il sistema con cui avrebbe potuto accertare la purezza o meno dell’oro della corona (Archimede avrebbe preparato due blocchi, uno d’oro e uno d’argento, ciascuno di peso uguale a quello della corona e li avrebbe immersi in acqua, misurando il volume d’acqua spostata da ciascuno e la relativa differenza; poi avrebbe accertato se la corona avesse spostato un volume d’acqua uguale a quello spostato dal blocco d’oro; se non fosse accaduto questo, ciò avrebbe significato che l’oro della corona era stato alterato). Per l’entusiasmo della scoperta si precipitò fuori dalla tinozza, corse a casa nudo com’era, gridando “l’ho scoperto, l’ho scoperto”, che in greco si dice éureka, esclamazione che divenne proverbiale e che resta tuttora in uso.
Sul procedimento usato da Archimede si discusse a lungo, dato che Vitruvio è molto generico. Galilei esordirà proprio con uno scritto su questo tema: Discorso del S. Galileo Galilei intorno all’arteficio che usò Archimede nel scoprir il furto dell’oro nella corona di Hierone.

La figura di Erone Fra i matematici e ingegneri del mondo antico va menzionato Erone , cui è attribuita una serie di scoperte. Purtroppo i dati della sua vita sono sconosciuti. Erone può collocarsi fra il III secolo a.C. e il I d. C. La questione è complicata dal fatto che: a) Erone era un nome comune e b) con esso si designava anche l’ingegnere come tale. Forse ciò che ci è pervenuto sotto il nome di Erone non è opera di un unico autore. Sembra certo che molto di ciò che va sotto il nome di Erone appartenga all’età ellenistica. La questione eroniana attende ancora, in ogni caso, di essere risolta in maniera soddisfacente.

◗ L’astronomia: Aristarco e Ipparco

Gli astronomi Eudosso, Callippo ed Eraclide Pontico La concezione astronomica dei Greci – fatte salve alcune eccezioni di cui diremo – fu geocentrica. Si immaginava che intorno alla Terra ruotassero le stelle, il Sole, la Luna e i pianeti con moto circolare perfetto. Si pensò, così, che ci dovessero essere una sfera che conducesse le cosiddette stelle fisse e una sfera per ciascun pianeta, tutte concentriche rispetto alla Terra. Ricordiamo che pianeta (dal greco plànomai, che vuol dire “vado errando”) significa “stella errante”, ossia stella che presenta movimenti complessi e apparentemente non regolari (donde appunto il nome).
Già Platone aveva compreso che non era sufficiente, per spiegare il moto dei pianeti, una sola sfera per ciascuno.
Il suo contemporaneo Eudosso (vissuto nella prima metà del IV secolo a.C. ), che fu l’ospite scienziato più illustre dell’Accademia, cercò la soluzione del problema. Bisognava spiegare, tenendo ferma l’ipotesi del moto circolare perfetto delle sfere che conducono i pianeti, quante ne occorressero per dar conto delle loro apparenti anomalie (il loro apparente regolare avvicinarsi, il loro spostarsi a destra e a sinistra secondo la latitudine). L’ipotesi di Eudosso fu di [pag.361] carattere geometrico e davvero ingegnosissima: egli introdusse, per spiegare le anomalie dei pianeti, tanti moti sferici quanti, combinandosi fra loro, potevano dare come risultato gli spostamenti degli astri che noi osserviamo.
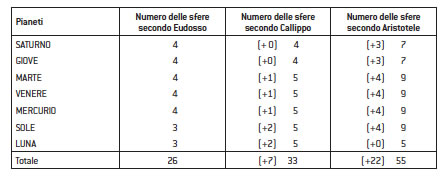
In tutto, quindi, Eudosso suppose 26 sfere. Egli non si preoccupò dei rapporti delle sfere motrici di ciascun pianeta con quelle del successivo e degli eventuali influssi delle une sulle altre. Forse, egli pensava il complesso sistema come un’ipotesi geometrico-matematica e non fisicizzava le sfere.
Il discepolo Callippo ritenne necessario aumentare di sette il numero delle sfere, che divennero 33. Aristotele , dal canto suo, introducendo l’elemento celeste dell’etere, fisicizzò il sistema e dovette, di conseguenza, introdurre sfere reagenti con moto a ritroso destinate a neutralizzare l’effetto delle sfere del pianeta superiore su quelle del pianeta inferiore. E queste sfere con moto a ritroso, troviamo essere tante quante quelle dei movimenti supposti necessari per ciascun pianeta, meno una. Si otteneva, così, il numero di 55. Lo schema costituisce un quadro sinottico illustrativo dei sistemi astronomici di Eudosso, Callippo e Aristotele .

Un tentativo veramente nuovo e originale fu fatto da Eraclide Pontico , contemporaneo di Eudosso, il quale suppose che “la Terra è sita nel centro e ruota”, “mentre il cielo sta fermo”. Secondo un’antica testimonianza (peraltro non del tutto sicura) Eraclide suppose anche, per spiegare alcuni fenomeni che l’ipotesi di Eudosso non spiegava, che Venere e Mercurio ruotassero circolarmente attorno al Sole, a sua volta ruotante intorno alla Terra. Ma la tesi non ebbe successo, almeno immediatamente.

Aristarco di Samo, il “Copernico antico”: le sue tesi e le ragioni che ne ostacolarono il successo Fu nella prima metà del III secolo a.C. (e quindi nell’epoca ellenistica di cui ci stiamo occupando), che si ebbe il tentativo più rivoluzionario dell’antichità, a opera di Aristarco di Samo , detto “il Copernico antico”. Egli suppose, come riferisce Archimede, «che le stelle fisse stiano immutabili e che la Terra giri attorno al Sole descrivendo un cerchio». Come si vede, Aristarco riprende l’idea di Eraclide Pontico ; ma si spinge oltre, sostenendo che il Sole è il centro intorno al quale ruotano tutti gli astri. Egli pare concepisse l’idea di un cosmo infinito; diceva infatti che la sfera delle stelle fisse, che ha come centro lo stesso centro del Sole, era così grande, che il cerchio secondo il quale si muoveva la Terra stava alla distanza delle stelle fisse «come il centro di una sfera sta alla sua superficie». Il che significa, appunto, a distanza infinita.
Un solo astronomo seguì la tesi di Aristarco e fu Seleuco di Seleucia (fiorito intorno al 150 a.C. ). Per contro, Apollonio di Perga, il grande matematico di cui abbiamo già parlato, e soprattutto Ipparco di Nicea, bocciarono la tesi e reimposero il geocentrismo che resistette fino a Copernico .
Le ragioni che ostacolarono il successo della tesi eliocentrica sono numerose:
• l’opposizione religiosa;
• l’opposizione delle sette filosofiche, comprese quelle ellenistiche;
• la difformità rispetto al sentire del senso comune, che trova molto più naturale il geocentrismo;
• alcuni fenomeni che sembravano rimanere inspiegati. [pag.362]
Sarebbe sufficiente eliminare le complicazioni apportate da Eudosso con la moltiplicazione del numero delle sfere e sostituirle con nuove ipotesi che, pur mantenendo il generale impianto geocentrico e le orbite circolari dei pianeti, potevano bene “salvare i fenomeni”, come si diceva allora, ossia spiegare ciò che appare alla visione e all’esperienza. Queste ipotesi si riducono a due molto importanti:
• quella degli epicicli (anticipata in qualche misura forse già da Eraclide);
• quella degli eccentrici.
La prima consisteva, come già accennato, nell’ammettere che i pianeti ruotassero intorno al Sole, che, a sua volta, ruotava intorno alla Terra. La seconda consisteva nell’ammettere orbite circolari attorno alla Terra aventi un centro non coincidente con il centro della Terra, e, quindi, appunto “eccentrico” rispetto a questa.

Ipparco di Nicea e i consensi da lui riscossi - Ipparco di Nicea , attivo verso la metà del II secolo a.C. , diede la spiegazione più convincente, per la mentalità di allora, dei moti degli astri sulla base di queste ipotesi. Ad esempio, la diversa distanza del Sole dalla Terra e le stagioni sono spiegabili facilmente, supponendo che il Sole ruoti secondo un’orbita eccentrica rispetto alla Terra. E, con abili combinazioni delle due ipotesi, riuscì a dar conto di tutti i fenomeni celesti. In questo modo il geocentrismo fu salvo, e, insieme, nessun fenomeno celeste sembrò restare senza spiegazione. Così Plinio loda il nostro astronomo: «Lo stesso Ipparco, che non sarà mai elogiato abbastanza, giacché nessuno più di lui ha dimostrato che l’uomo ha affinità con gli astri e che le nostre anime sono parti del cielo, scoprì una stella nuova e differente nata al suo tempo. E constatando che il luogo in cui rifulgeva si spostava, si pose il problema se questo non dovesse aver luogo più di frequente, e se le stelle che riteniamo fisse non si muovessero esse pure: di conseguenza, osò gettarsi in una impresa che sarebbe improba perfino per un dio, quella di contare le stelle per i posteri e di catalogare gli astri, mediante strumenti da lui inventati, mediante i quali poteva indicare le loro posizioni e grandezze in modo che si potesse facilmente riconoscere di qui, non solo se le stelle morissero e nascessero, ma anche se qualcuna si spostasse o si muovesse, se crescesse o diminuisse. E così lasciò in eredità il cielo a tutti gli uomini, nel caso che si trovasse un uomo che fosse in grado di raccoglierne l’eredità». E in eredità lasciò un catalogo di ben 850 stelle!

◗ Apogeo e involuzione della medicina ellenistica

Nella prima metà del III secolo a.C. nel Museo si effettuarono ricerche di anatomia e di fisiologia molto importanti, soprattutto a opera dei medici Erofilo di Calcedonia ed Erasistrato di Iulide . La possibilità di dedicarsi alla ricerca finalizzata al puro incremento del sapere, le attrezzature messe a disposizione dal Museo e la protezione di Tolomeo Filadelfo, che permise la dissezione di cadaveri, fecero compiere progressi notevolissimi a tali scienze. È certo che Erofilo ed Erasistrato si spinsero addirittura a operazioni di vivisezione su alcuni malfattori (con permesso regio), suscitando scalpore.
A Erofilo si debbono molte scoperte nell’ambito dell’anatomia descrittiva (alcune portano ancora il suo nome). Egli superò definitivamente la concezione che l’organo centrale dell’organismo vivente fosse il cuore e dimostrò che era, invece, il cervello. Riuscì altresì a stabilire la distinzione fra nervi sensori e nervi motori. Erofilo, riprendendo un’idea del maestro Prassagora, studiò le pulsazioni e ne indicò il valore diagnostico. Riprese, infine, la dottrina degli umori di genesi ippocratica.
Erasistratoa:Erasistrato di Iulide: distinse le arterie dalle vene e sostenne che le prime contengono l’aria, mentre le seconde il sangue. Gli studiosi di storia della medicina hanno spiegato l’equivoco, chiarendo: a) che, con arteria, i Greci indicavano anche la trachea e i bronchi e b) che negli animali morti (che venivano sezionati) il sangue trapassa dalle arterie alle vene. Le sue spiegazioni fisiologiche adottarono criteri ispirati al meccanicismo (specie di Stratone di Lampsaco ). Ad [pag.363] esempio, tutta la digestione veniva spiegata in funzione della meccanica dei muscoli, mentre l’assorbimento del nutrimento da parte del tessuto veniva spiegato col principio che passò alla storia come principio dell’horror vacui, secondo cui la natura tende a riempire ogni vuoto.
Questo momento di gloria non durò a lungo. Già Filino di Cos, un discepolo di Erofilo, si staccò dal maestro, e, probabilmente sotto l’influsso dello Scetticismo, aprì la strada a quella Scuola che verrà chiamata dei medici empirici, che rifiutavano il momento teoretico della medicina, per affidarsi alla sola esperienza. Serapione di Alessandria consolidò questo indirizzo, che ebbe lunga fortuna fino a che, in età cristiana, si fuse, a opera di Menodoto, con il Neoscetticismo. Ricordiamo, da ultimo, che la dottrina di Erasistrato, secondo cui nelle arterie circola aria, costituisce un antecedente di quella tendenza della medicina che, soprattutto sotto l’influsso della Stoà, darà molto rilievo al pneuma, fluido vitale di natura aerea che si inspira con l’aria (“medicina pneumatica”). Ma avremo modo di esaminare la più sofisticata formulazione di questa dottrina, sintetizzata con la tradizionale dottrina umorale, quando parleremo di Galeno .

◗ La geografia: Eratostene

La geografia ebbe la sua sistemazione nell’opera di Eratostene . Egli fu chiamato nel 246 a.C. dal re Tolomeo II ad Alessandria come direttore della Biblioteca, come già abbiamo ricordato, e fu amico di Archimede . Fu versato in molti campi del sapere, ma non al punto da imporsi in modo perentorio. Il suo merito storico resta quello di aver applicato la matematica alla geografia e di aver disegnato la prima carta del mondo seguendo il criterio dei meridiani e dei paralleli. Eratostene riuscì anche, basandosi su calcoli ingegnosi e impostati con correttezza metodologica, a calcolare le dimensioni della Terra. Il risultato che ottenne fu di 252. 000 stadi (pari a circa 39. 960 chilometri). Nell’antichità il valore dello stadio non era uniforme; ma, se è vero che lo stadio adottato da Eratostene era quello di 157,5 metri, la cifra che ne risulta è di poche decine di chilometri inferiore a quella che oggi si calcola.
[pag.364]

3. Conclusioni sulla scienza ellenistica

◗ La specializzazione come carattere peculiare della scienza ellenistica

Come si è già avuto modo di vedere dall’esposizione della scienza ellenistica nei suoi differenti settori, ci troviamo di fronte a un fenomeno in larga misura nuovo, sia nella qualità sia nell’intensità. Gli storici della scienza hanno ben rilevato che la nota definitoria del fenomeno sta nel concetto di specializzazione. Il sapere si differenzia nelle sue “parti” e cerca di definirsi nell’ambito di ciascuna di queste in maniera autonoma, ossia con logica propria e non come semplice applicazione della logica dell’intero in cui rientrano le parti.
Questa specializzazione, secondo il comune modo di intendere questo fenomeno, suppone un duplice affrancamento:
• dalla religione tradizionale o comunque da un tipo di mentalità religiosa che assume come invalicabili certi limiti in determinati ambiti;
• dalla filosofia e dai relativi dogmi.
Ora, questo è indubbiamente vero, ma occorre fare qualche precisazione.
• La libertà religiosa di cui in Grecia hanno sempre goduto i pensatori è innegabile. Va peraltro riconosciuto che la dissezione di cadaveri e la vivisezione su uomini in Atene sarebbero state impossibili, e solo con la protezione dei Tolomei e in un ambiente come Alessandria, spregiudicato e paradossalmente collocato in un Egitto ancora chiuso in strutture orientali, divenne possibile.
• Anche l’indipendenza dalla filosofia è vera, ma essa pure non va esagerata, anzi va ridimensionata. I sistemi ellenistici, come abbiamo visto, sono i più dogmatici che il mondo antico abbia avuto. Epicuro, non meno della Stoà, sosteneva che il sapiente deve avere “dogmi” e che questi dogmi sono intoccabili. Il fatto che AteneAlessandria: diventasse la capitale della scienza, e che fra le due città ci fosse una tale distanza, mise la scienza alessandrina al riparo da quei dogmi e la lasciò libera nel suo esplicarsi.
Tuttavia, non si insisterà mai abbastanza sul fatto che furono dei peripatetici, quali Demetrio Falereo e Stratone di Lampsaco, a progettare un’organizzazione che riproducesse il Peripato in grande. E poiché Demetria:Demetrio_Falereo: o era stato discepolo di Teofrasto, lo scienziato del Peripato, quella scissione che molti sottolineano non va esagerata. Del resto Aristotele medesimo diede prova di saper condurre ricerche con metodo empirico rigoroso (nella Storia degli animali, nella sua Raccolta delle costituzioni), ricerche che furono continuate da Teofrasto nella botanica, cosicché la ricerca specializzata alessandrina ha i suoi antecedenti proprio nel Peripato. Si potrebbe dire che, in linea di principio, avverso a ricerche specialistiche era il nuovo spirito delle nuove Scuole ellenistiche, ma non l’antico spirito aristotelico.
Resta, in ogni caso, il fatto che la nota essenziale che ha caratterizzato la scienza è stata la specializzazione, perseguita senza il bisogno dell’elaborazione di uno sfondo filosofico, anzi con la esplicita messa in parentesi di questo sfondo.

◗ Lo spirito teorico della scienza greco-ellenistica

Ma c’è un altro punto molto importante da rilevare. La scienza specialistica alessandrina non solo si affrancò dai pregiudizi religiosi e dai dogmi filosofici, ma volle assumere una propria autonoma identità anche nei confronti della “tecnica”, con cui, invece, se dovessimo giudicare con la mentalità di oggi, parrebbe naturale pensare che dovesse stringere un’alleanza.
La scienza ellenistica sviluppò l’aspetto teorico delle scienze particolari e solo questo, disprezzando il momento applicativo-tecnico nel senso moderno. La mentalità tecnologica è [pag.365] quanto di più distante si possa pensare dall’antica scienza. Si suole citare l’atteggiamento di Archimede nei confronti delle proprie scoperte nel campo della meccanica, che egli interpretava, se non come svago, certo come un momento marginale della sua vera attività, che era quella del matematico puro.
Ci si è domandati il perché di questo fatto, che a noi sembra tanto innaturale. La risposta è stata, per lo più, ricercata nelle condizioni socio-economiche del mondo antico: lo schiavo stava al posto della macchina e il padrone non aveva bisogno di congegni particolari per evitare fatiche o risolvere problemi pratici. Inoltre, poiché del benessere beneficiava solo una minoranza, non era necessario uno sfruttamento intensivo né della produzione agricola, né di quella artigianale. Insomma: la schiavitù e la discriminazione sociale sarebbero lo sfondo che rende comprensibile la non necessità delle macchine. Viene ricordata, a questo proposito, la distinzione di Varrone fra tre tipi di strumenti:
• quelli parlanti (gli schiavi);
• quelli parlanti a metà (i buoi);
• quelli muti (gli strumenti meccanici).
Ma questo era stato addirittura teorizzato da Aristotele: «l’operaio nelle tecniche rientra nella categoria degli strumenti», «lo schiavo è una proprietà animata e ogni operaio è come uno strumento che precede e condiziona gli altri strumenti». Tutto questo è senza dubbio fondamentale per spiegare i fenomeni che stiamo studiando.
Ma il punto chiave è un altro. La scienza ellenistica fu quella che fu, perché, pur cambiando l’oggetto dell’indagine rispetto alla filosofia (concentrandosi sulle “parti”, anziché sull’“intero”), mantenne lo spirito della vecchia filosofia, lo spirito “contemplativo” che i Greci chiamavano “teoretico”.
Lo spirito del vecchio Talete che, come si narra, cadde nella fossa, tutto intento a contemplare il cielo e che Platone additava come simbolo del più autentico spirito teoretico, c’è tutto intero in Archimede, in quel suo motto superiore Noli turbare circulos meos rivolto al soldato romano che stava per ucciderlo, e in quel suo gioioso «Éureka!». Così è presente in quell’aneddoto secondo cui Euclide, richiesto da uno di spiegargli a che cosa servisse la sua geometria, per tutta risposta gli fece dare del denaro, una specie di obolo, come si dà a un mendicante. E lo stesso Tolomeo presenterà la sua astronomia come la vera scienza nel senso dell’antica filosofia, e Galeno dirà che l’ottimo medico, per essere tale, dovrà essere filosofo. Insomma, la scienza greca è stata animata proprio da quella forza “teoretico-contemplativa” – da quella forza, cioè, che spingeva a considerare le cose visibili spiraglio attraverso cui si accede all’invisibile –, che la mentalità “pragmatico-tecnologica” moderna parrebbe aver dissolto, o perlomeno emarginato.